Definition of a Function

A function takes an input x and outputs a value y.

Domain

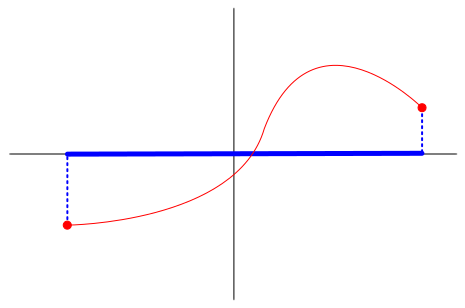
The domain describes all possible values x that a function can take as an input.

Range

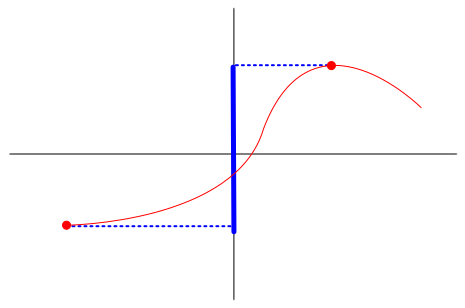
The range describes all the possible values f(x) that a function can output.

Vertical Line Test

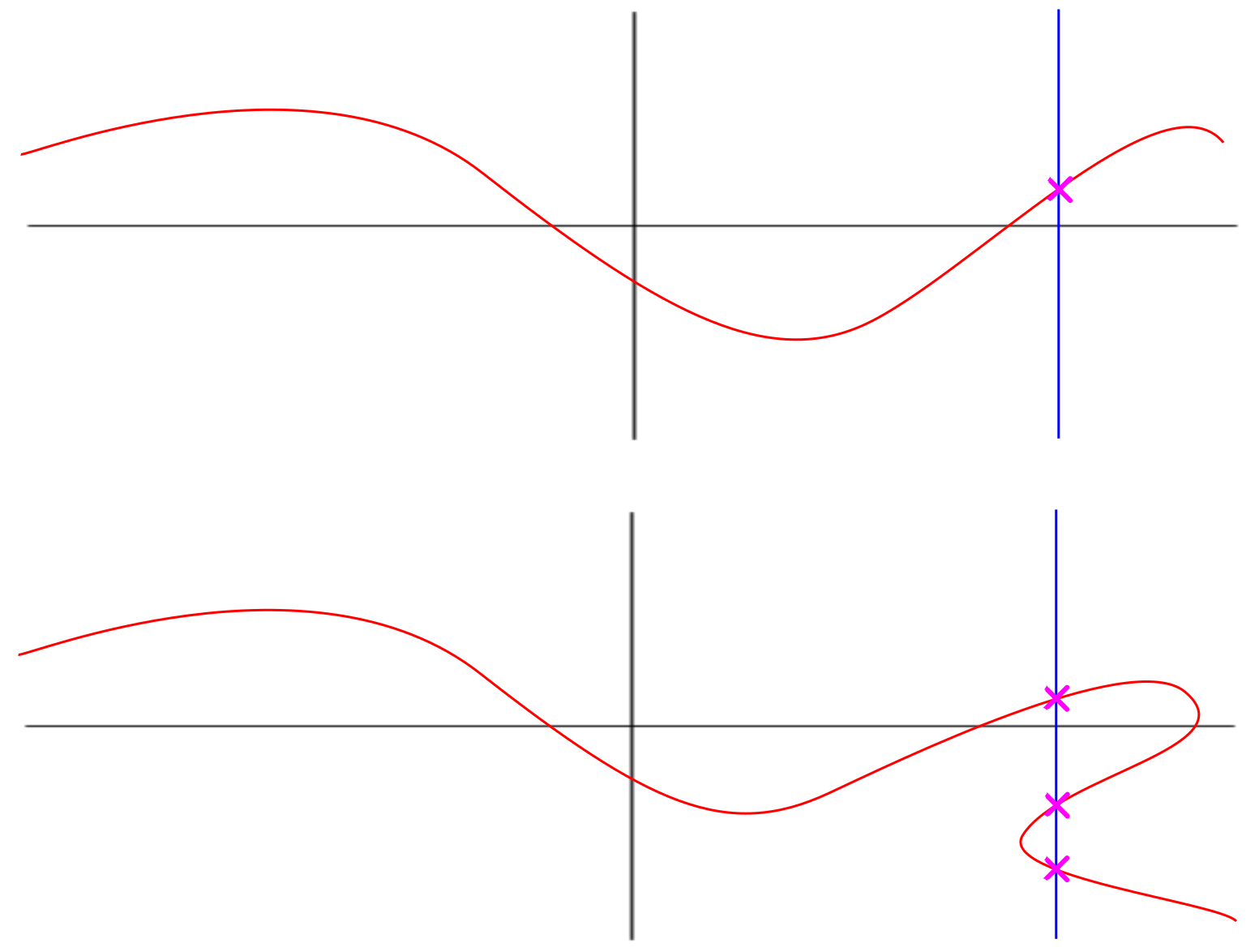
The graph of a valid function only touches a vertical line once anywhere in its domain.

Even Functions

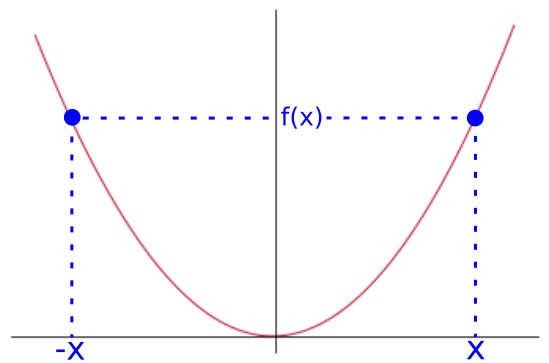
An even function is a function such that f(-x)=f(x). Visually this is a function that is reflected across the y-axis.

Odd Functions

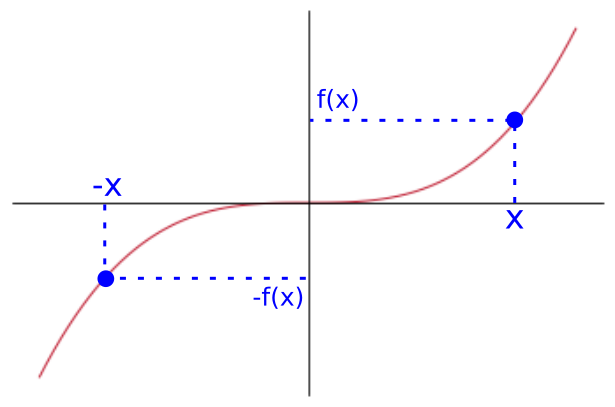
An odd function is a function such that f(-x)=-f(x). Visually this is a function that is reflected across the origin.

Increasing Functions

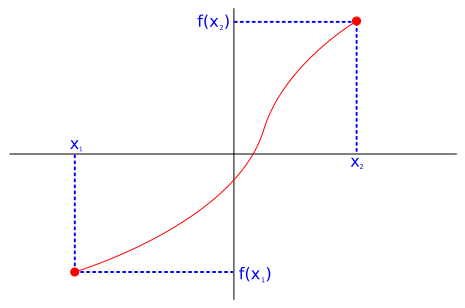
A function is increasing in range if for every value x₁<x₂, f(x₂)>f(x₁).

Decreasing Functions

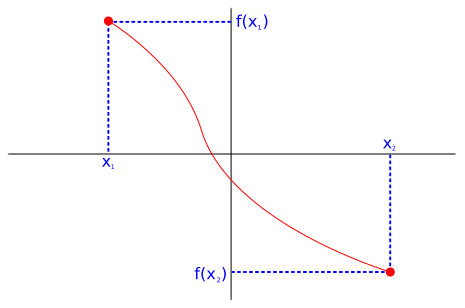
A function is decreasing in range if for every value x₁<x₂, f(x₁)>f(x₂).

Inverse Function

The inverse function takes the dependent variable from the original function and returns the independent variable. The range of a function is the domain of its inverse and vice versa.

Composition of Functions

The composition "f of g" means that x is first put through the function g(x), then the output of that is put through the function f(x).

Inverse Function Composition

The inverse of a function is a function that it completely reverses the effects of another function when the two are composed together throughout a specified range.

Function Operations

One-to-One Function

A function is one-to-one if and only if it does not output the same value for two separate inputs. A function must be one-to-one within a specified range for it to have an inverse.

Horizontal Line Test

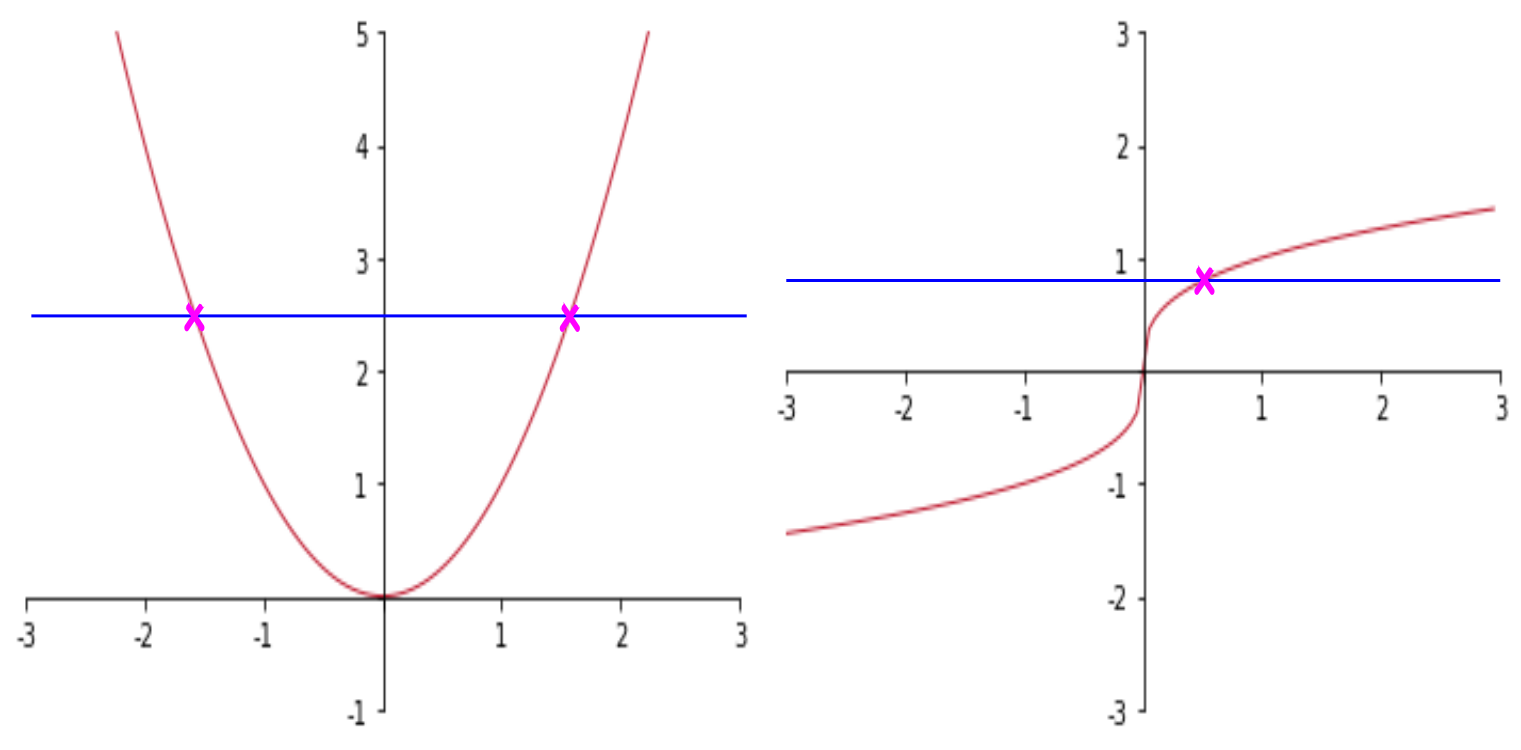
A function is one-to-one within a range if its graph does not touch a horizontal line more than once along its range.

Function

Vertical Translation (Up)

Vertical Translation (Down)

Horizontal Translation (Left)

Horizontal Translation (Right)

Vertical Scaling (Squash)

Vertical Scaling (Pull)

Horizontal Scaling (Squash)

Horizontal Scaling (Pull)